特殊四邊形主要包括平行四邊形、矩形、菱形、正方形和梯形.在解決一些和四邊形有關的問題時往往需要添加輔助線,此篇文章介紹一些輔助線的添加方法,原文於對岸網站流傳甚廣,出處已不可考。
一、 和平行四邊形有關的輔助線作法
平行四邊形是最常見的特殊四邊形之一,它有許多可以利用性質,為了利用這些性質往往需要添加輔助線構造平行四邊形.
[@more@]
1.利用一組對邊平行且相等構造平行四邊形
例1 、如圖1,已知點O是平行四邊形ABCD的對角線AC的中點,四邊形OCDE是平行四邊形.
求證:OE與AD互相平分.
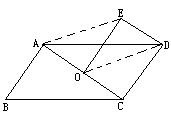
分析:
因為四邊形OCDE是平行四邊形,所以OC//ED,OC=DE,又由O是AC的中點,得出AO//ED,AO=ED,則四邊形AODE是平行四邊形,問題得證.
證明:連結AE、OD,因為是四邊形OCDE是平行四邊形,所以OC//DE,OC=DE,因為0是AC的中點,所以A0//ED,AO=ED,所以四邊形AODE是平行四邊形,所以AD與OE互相平分.
說明:當已知條件中涉及到平行,且要求證的結論中和平行四邊形的性質有關,可試通過添加輔助線構造平行四邊形.
2.利用兩組對邊平行構造平行四邊形
例2、如圖2,在△ABC中,E、F為AB上兩點,AE=BF,ED//AC,FG//AC交BC分別為D,G.求證:ED+FG=AC.
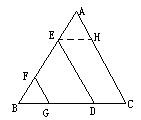
分析:要證明ED+FG=AC,因為DE//AC,可以經過點E作EH//CD交AC於H得平行四邊形,得ED=HC,然後根據三角形全等,證明FG=AH.
證明:過點E作EH//BC,交AC於H,因為ED//AC,所以四邊形CDEH是平行四邊形,所以ED=HC,又FG//AC,EH//BC,所以∠AEH=∠B,∠A=∠BFG,又AE=BF,所以△AEH≌△FBG,所以AH=FG,所以FG+DE=AH+HC=AC.
說明:當圖形中涉及到一組對邊平行時,可通過作平行線構造另一組對邊平行,得到平行四邊形解決問題.
3.利用對角線互相平分構造平行四邊形
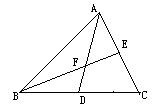
例3 、如圖3,已知AD是△ABC的中線,BE交AC於E,交AD於F,且AE=EF.求證BF=AC.
分析:要證明BF=AC,一種方法是將BF和AC變換到同一個三角形中,利用等邊對等角;另一種方法是通過等量代換,尋找和BF、AC相等的相段代換.尋找相等的線段的方法一般是構造平行四邊形.
證明:延長AD到G,使DG=AD,連結BG,CG,因為BD=CD,所以四邊形ABGC是平行四邊形,所以AC=BG,AC//BG,所以∠1=∠4,因為AE=EF,所以∠1=∠2,又∠2=∠3,所以∠1=∠4,所以BF=BG=AC.
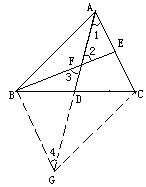
說明:本題通過利用對角線互相平分構造平行四邊形,實際上是採用了平移法構造平行四邊形.當已知中點或中線應思考這種方法.
二、和菱形有關的輔助線的作法
和菱形有關的輔助線的作法主要是連接菱形的對角線,藉助菱形的判定定理或性質定定理解決問題.
例4 、如圖5,在△ABC中,∠ACB=90°,∠BAC的平分線交BC於點D,E是AB上一點,且AE=AC,EF//BC交AD於點F,求證:四邊形CDEF是菱形.
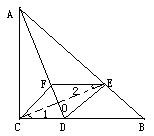
分析:要證明四邊形CDEF是菱形,根據已知條件,本題有兩種判定方法,一是證明四邊相等的四邊形是菱形,二是證明對角線互相垂直平分的四邊形是菱形.根據AD是∠BAC的平分線,AE=AC,可通過連接CE,構造等腰三角形,藉助三線合一證明AD垂直CE.求AD平分CE.
證明:連結CE交AD於點O,由AC=AE,得△ACE是等腰三角形,因為AO平分∠CAE,所以AO⊥CE,且OC=OE,因為EF//CD,所以∠1=∠2,又因為∠EOF=∠COD,所以△DOC可以看成由△FOE繞點O旋轉而成,所以OF=OD,所以CE、DF互相垂直平分.所以四邊形CDEF是菱形.
例5、如圖6,四邊形ABCD是菱形,E為邊AB上一個定點,F是AC上一個動點,求證EF+BF的最小值等於DE長.
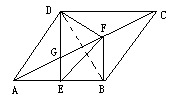
分析:要證明EF+BF的最小值是DE的長,可以通過連結菱形的對角線BD,藉助菱形的對角線互相垂直平分得到DF=BF,然後結合三角形兩邊之和大於第三邊解決問題.
證明:連結BD、DF.
因為AC、BD是菱形的對角線,所以AC垂直BD且平分BD,所以BF=DF,所以EF+BF=EF+DF≥DE,若且唯若F運動到DE與AC的交點G處時,上式等號成立,所以EF+BF的最小值恰好等於DE的長.
說明:菱形是一種特殊的平行四邊形,和菱形的有關證明題或計算題作輔助線的不是很多,常見的幾種輔助線的方法有:(1)作菱形的高;(2)連結菱形的對角線.
三、 與矩形有輔助線作法
和矩形有關的題型一般有兩種:
(1)計算型題,一般通過作輔助線構造直角三角形藉助勾股定理解決問題;
(2)證明或探索題,一般連結矩形的對角線藉助對角線相等這一性質解決問題.和矩形有關的試題的輔助線的作法較少.
例6、如圖7,已知矩形ABCD內一點,PA=3,PB=4,PC=5.求 PD的長.
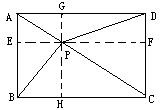
分析:要利用已知條件,因為矩形ABCD,可過P分別作兩組對邊的平行線,構造直角三角形藉助勾股定理解決問題.
解:過點P分別作兩組對邊的平行線EF、GH交AB於E,交CD於F,交BC於點H,交AD於G.因為四邊形ABCD是矩形,所以PF2=CH2=PC2-PH2,DF2=AE2=AP2-EP2,PH2+PE2=BP2,所以 PD2=PC2-PH2+AP2-EP2=PC2+AP2-PB2=52+32-42=18,所以 PD=3√2.
說明:本題主要是藉助矩形的四個角都是直角,通過作平行線構造四個小矩形,然後根據對角線得到直角三角形,利用勾股定理找到PD與PA、PB、PC之間的關係,進而求到PD的長.
四、與正方形有關輔助線的作法
正方形是一種完美的幾何圖形,它既是軸對稱圖形,又是中心對稱圖形,有關正方形的試題較多.解決正方形的問題有時需要作輔助線,作正方形對角線是解決正方形問題的常用輔助線.
例7、如圖8,過正方形ABCD的頂點B作BE//AC,且AE=AC,又CF//AE.求證:∠BCF=∠AEB.
分析:由BE//AC,CF//AE,AE=AC,可知四邊形AEFC是菱形,作AH⊥BE於H,根據正方形的性質可知四邊形AHBO是正方形,從AH=OB=AC,可算出∠E=∠ACF=30°,∠BCF=15°.
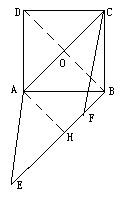
證明:連接BD交AC於O,作AH⊥BE交BE於H.在正方形ABCD中,AC⊥BD,AO=BO,又BE//AC,AH⊥BE,所以BO⊥AC,所以四邊形AOBH為正方形,所以AH=AO=AC,因為AE=AC,所以∠AEH=30°,因為BE//AC,AE//CF,所以ACFE是菱形,所以∠AEF=∠ACF=30°,因為AC是正方形的對角線,所以∠ACB=45°,所以∠BCF=15°,所以∠BCF=∠AEB.
說明:本題是一道綜合題,既涉及正方形的性質,又涉及到菱形的性質.通過連接正方形的對角線構造正方形AHBO,進一步得到菱形,藉助菱形的性質解決問題.