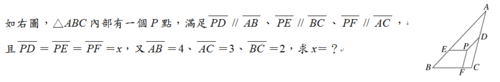國中九年級數學的相似形單元,有一些我覺得比較難的題目,曾寫了數題詳解在「九年級第一次段考範圍相似形數題」那篇網誌裡,當時用 Word 編輯後,轉檔為 swf 格式呈現於網頁,增加題目比較麻煩,新增的題目則記錄在這一篇。
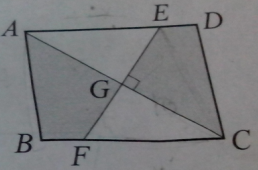
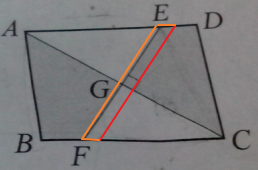
1. 如圖,矩形 ABCD 中,線段 AB=12,線段 BC=16,線段 EF 垂直線段 AC 於 G 點,則線段 EF=?
[@more@]這題的解題關鍵在於讓 G 點成為線段 AC 還有線段 EF 的中點。就算原題不在中點,只要將線段 EF 平行移動至線段 AC 的中點上就可以了。(因為平行移動時,能與原線段構成平行四邊形,對邊相等,不改變原本所求的 EF 長度。
2.
這題我覺得很難,詳解記錄如下:
3. 在△ABC中, 若∠A=2∠B, 邊AC=4, AB=5, 則邊長BC等於多少?
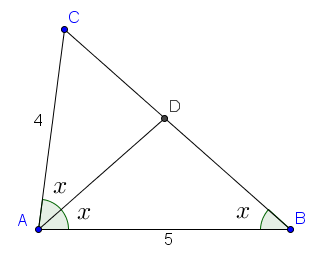
[解法1]
做 ∠A 的平分線, 如圖, 由內分比性質, AB:AC = BD:DC
而 △ABD 為等腰三角形, BD = AD, 所以 AB:AC = AD:DC
△ABC~△DAC (AA相似),
AC:CD = BC:AC → 4:4x = 9x:4 → x = 2/3
故 BC = 9*2/3 = 6
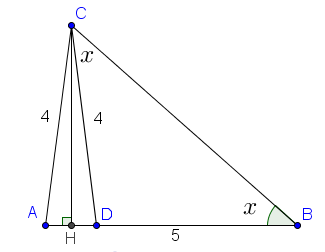
[解法2]
過 C 做 CH⊥AB, 交 AB 於 H, 在 AB 上取一點 D,
連接 CD, 使 CD=AC=4,
∵∠A=2∠B, 邊 AC=4, AB=5,
由大邊對大角, ∴∠ACB>∠ABC, 三角形只有最大的才可能是鈍角, 因此∠A 必是銳角.
∵CD=AC=4, ∴∠A=∠CDA=2∠B, ∴∠B=∠BCD
∴BD=CD=4, DH=AH=0.5
根據勾股定理,
BC² = BH²+CH² = BH²+AC²-AH² = ﹙4﹢0.5﹚²﹢4²-0.5² = 36
∴BC=6