各校的段考考古題中,有些較難的試題,學生要在 45 分鐘一節課的考試時間內要想到解法,數學能力應該很好,否則就是要事先看過或算過才有辦法。可能我的數學能力還不夠好,有時候想一陣子還想不到的時候,只好請教同事或是上網找答案,順便在此紀錄。
1. 如圖,在△ABC中,AB=AC,底角B的三等分線交高線AD於M、N,邊CN並延長交AB於E.求證:EM∥BN.
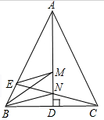
[@more@]
[Sol]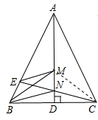
∵AB=AC,AD是高,
∴AD是等腰△ABC的中垂線
∴BN=CN;∠NBD=∠NCD
連接MC線段
∵∠BEC=∠BAC+∠ACE=∠BAC+2/3∠ABC
∠BMC=∠BAC+∠ABM+∠ACM=∠BAC+2/3∠ABC
∴∠BEC=∠BMC
∴B,C,M,E四點共圓
∴∠EMB=∠BCE=∠MBN
∴EM∥BN.
註:如果同一平面內的四個點在同一個圓上,則稱這四個點共圓(有圓內接四邊形),一般簡稱為“四點共圓”。四點共圓有三個性質:(1)共圓的四個點所連成同側共底的兩個三角形的頂角相等;(2)圓內接四邊形的對角互補;(3)圓內接四邊形的外角等於內對角。以上性質可以根據圓周角等於它所對弧的度數的一半進行證明。(From 百度百科)