在昌爸工作坊的討論區看到有人詢問五題幾何類問題的作法,這幾題都是難題,為免以後那個網頁消失不見,因此在此做個備份。題目如下:
1.
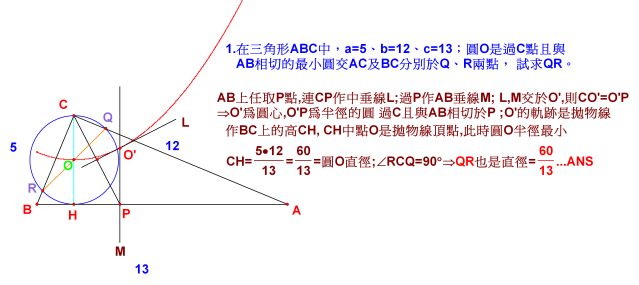
在三角形ABC中,a=5、b=12、c=13;圓O是過C點且與AB相切的最小圓交AC及BC分別於Q、R兩點,試求QR。
2.
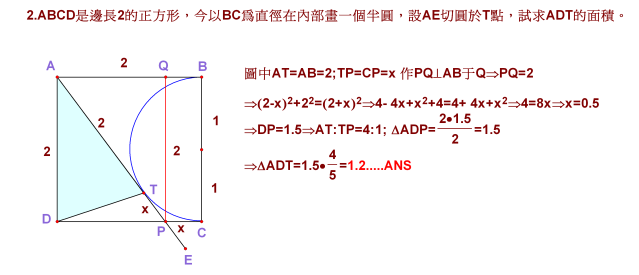
ABCD是邊長2的正方形,今以BC為直徑在內部畫一個半圓,設AE切圓於T點,試求ADT的面積。
3.
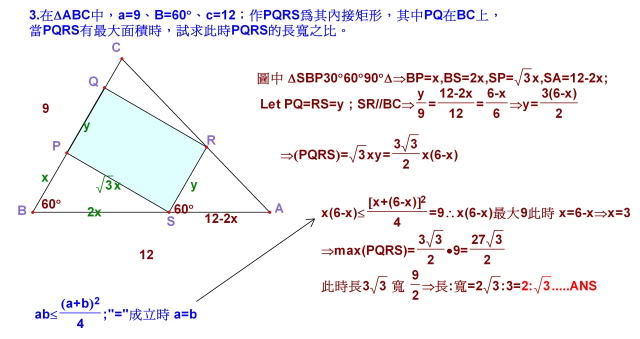
在三角形ABC中,a=9、B=60度、c=12;作PQRS為其內接矩形,其中PQ在BC上,當PQRS有最大面積時,試求此時PQRS的長寬之比。
4.
ABCD是等腰梯形,AB//DC且AD=BC=根號3;若對角線相交於O點,且角AOB=60度,E、F分別為OA、BC的中點,試求EF。
5.
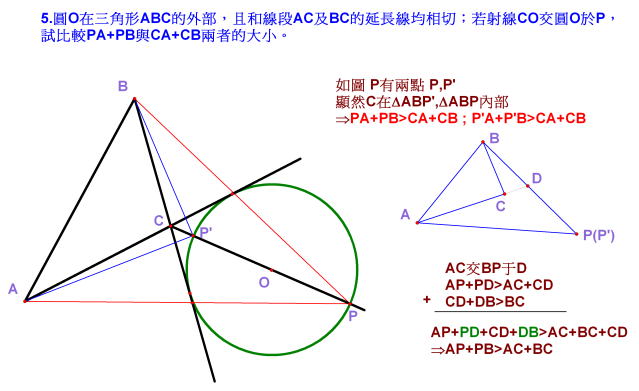
圓O在三角形ABC的外部,且和線段AC及BC的延長線均相切;若射線CO交圓O於P,試比較PA+PB與CA+CB兩者的大小。
詳解如下:
[@more@]

[另解]
ABCD為等腰梯形,角BAO=角ABO,需要講原因嗎??
又角AOB=60度,180-60=120,120/2=60,三角形A0B內角皆為60度,為正三角形
E為OA中點,三角形A0B為正三角形,角BEC=90度,B,E,C三點共圓,BC為直徑
F為BC中點,CF=EF=BF=(根號3)/2